I was sooo happy when we installed the new monitor system in the project studio. Hey, now we can start mixing since these monitors are great! Full spectrum frequencies, not leaving out half of them like the old system. 🙂
Mmmh, but then it turned out, that the new system was “too good” for the room. Why? Well, when turning it louder, we had a deep “huuum” in the room. Not always, but sometimes. Often. Very often! What was that? Ok, measure microphone connected, pinknoise on, analyse running and this is what it looked like:
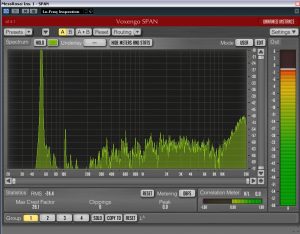
OMG, a spike that was going through the roof at around 53Hz.
Called a friend who is a professional sound engineer/master/godfather of sound, and told him the results. He immediately asked for the room size, I told him 3,20m x something 5-6m or so. He quickly calculated and said that a full soundwave that would fit in 3,20m would be around 106Hz. Told him, that we have a peak at 53Hz, not 106Hz. So we discussed and agreed, it was the octave down, so half wave length of 53Hz. Mmmh, let’s calculate again:
106Hz: For sound wave, wavelength (λ) in Air is nearly 3.238 meter
53Hz: For sound wave, wavelength (λ) in Air is nearly 6.475 meter
Half a wavelength is what is called 1st harmonic and so we had a standing wave due to the size of the room, better, due to the distances between the walls where the monitor system was installed. (Standing wave in an open pipe)
We discussed resonators, since it would be impossible to tear down the walls in the basement (where the project studio is located), but unfortunately, the standard resonators start operating at around 100Hz going up, and we have a problem at 53Hz. He pointed out, that he worked with Helmholtz resonators and that these could operate below 100Hz, but never built one of these.
OK, “Helmholtz resonator”, never heard of it, so I decided to do a research on the internet. It turned out, that there are tons of wrong formulas for this, took me a few days and nights until I found someone pointing to the correct formula, who also said, there are way too many wrong formulas on the internet. So, here is the one I used:
F = [c / (2 * 兀)] * √ [SR /(V * (RL + 2ΔL)]*100
c= speed of sound, which is defined 343,2 m/s (1236 km/h) at 20° Celsius
We should be safe if we use 343 for c. 🙂
F = [343 / (2 * 兀)] * √ [SR /(V * (RL + 2ΔL)]*100
F is the resonanzfrequency,
兀 is number Pi so 3,14..
SR is the Mouth surface of the pipe, so SR = Pi * r²
V is the volume
r is therefore radius of the pipe in cm
RL is the length of the pipe in cm
2ΔL (2DeltaL) is the muzzle correction, which is always 1.6 * r
However, once I had the correct formula, I created a “test balloon” resonator, simply out of pressboard, held together with tape. I must admit, I didn’t want a cube because of a lack of space, so I went for a triangular form that would fit nice into the corner.

So, once “installed”, measure microphone, pinknoise and……..hey, it came down a bit. So, the resonators are working, they’re just way too small.
Based on the results, we would roughly need a volume of 400ltr to eliminate the standing wave. I was too afraid to use an adjustable pipe, so I calculated the pipe as the thickness of the plate that the resonators would be build of. 🙂
And here they are, 99.452ltr volume each:


And guess what? They’re doing the job. Here’s the low frequency inspection with the resonators installed:
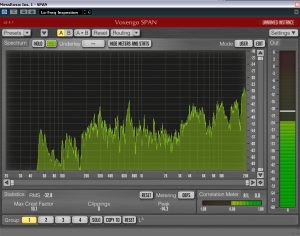
No more peak at 53Hz, also the rest leveled much better than before.
Yet another DIY to understand a little bit more of what’s going on. 🙂
